在算法交易的领域中，机器学习的广泛应用，促使数据挖掘技术被用来发掘金融数据中的隐藏模式。在这一背景下，从业人员经常面临挑战，即如何从众多变量中筛选出最有可能对实现特定目标或解决特定问题有用的变量。本文探讨了特征选择算法的实现，该算法旨在评估一组候选变量在给定预测任务中的相关性。MT5官方版软件下载为交易者提供了一个强大的平台，使其能够利用机器学习技术来优化交易策略。

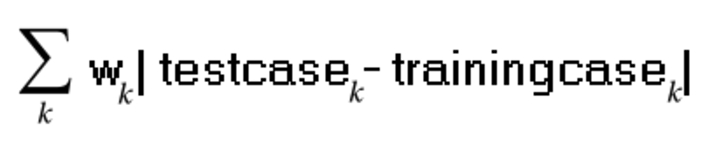
　　特征选择算法的核心在于评估变量的相关性，从而提高预测模型的准确性和效率。FREL（Feature Selection using Energy-based models）背后的概念灵感来源于一种被称为加权最近邻分类的技术，该技术利用数据集中点之间的距离来进行预测。通过为每个特征确定适当的权重，这种方法可以提高预测的准确性。

　　加权最近邻分类是k-最近邻（k-NN）算法的一种变体，k-NN算法是机器学习领域中用于分类任务的常用方法。在标准的k-NN分类中，算法在分类新数据点时，会查看训练集中k个最近的数据点，最终将这些邻居中的多数类别分配给新数据点。然而，在加权最近邻分类中，不是仅仅统计最邻近数据的投票量，而是根据每个邻近数据与新数据点的距离为其投票加权。其原理是，较近的相邻数据应该对分类决策产生更大的影响，而较远的则影响较小。

　　这个加权过程涉及计算新数据点与训练集中每个点之间的距离。常用的距离度量包括欧几里得距离、曼哈顿（Manhattan）距离或余弦相似度，具体选择取决于数据的特性。在这种情况下，我们使用曼哈顿距离（也称为城市街区距离）来计算数据点之间的距离。计算这个距离的公式如下所示，其中，w表示权重，测试用例是相对于其他训练数据进行评估的，这些训练数据被称为训练案例。

　　机器学习中的基于能量的模型是一个多功能的框架，既适用于有监督学习任务，也适用于无监督学习任务。它的工作原理是为各种数据配置分配能量值，并学习一个能够区分理想配置和不理想配置的模型。这是通过最小化观测数据的能量，同时最大化未观测数据或不理想数据配置的能量来实现的。

　　基于能量的模型的核心在于定义一个能量函数，用E()表示。这个函数以输入变量的配置（或称为预测变量）以及一组模型参数作为输入。能量函数的输出是输入变量配置相关性的指征。例如，在评估回归模型的背景下，能量函数可以表示为均方误差。当将相关预测变量输入到均方误差方程中时，输出值往往较小，这反映了较高的相关性。相反，较差的预测变量会导致较大的均方误差值。能量函数为每个可能的变量配置分配一个标量值。

　　训练能量基模型的目标是学习能量函数的参数，以便为相关输入变量分配低能量，为不相关输入变量分配高能量。这包括定义一个目标函数，该函数会对为正确变量分配高能量，对错误变量分配低能量的情况进行惩罚。为了实现这一点，目标是识别出产生最低能量的错误变量配置，这种配置很可能导致模型做出错误的预测。面的函数表示输入配置x和模型参数w的能量，该能量输出错误的值y，这个值太低，以至于无法与产生准确预测的输入变量配置区分开来。

　　通过上述讨论，我们可以看到机器学习在算法交易中的巨大潜力，特别是在特征选择和模型优化方面。MT5官方版软件下载为交易者提供了一个集成的环境，使其能够利用这些先进的技术来提高交易效率和盈利能力。通过结合机器学习算法和MT5平台的强大功能，交易者可以更好地理解和预测市场动态，从而制定出更精准的交易策略。